更多“设u=a-b+2c,v=-a+3b-c.试用a、b、c表示2…”相关的问题
更多“设u=a-b+2c,v=-a+3b-c.试用a、b、c表示2…”相关的问题
设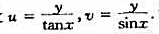 证明:当
证明:当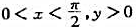 时,u,v可以用采作为曲线坐标;解出x,y作为u,v的函数;曲出xy平面上u=1,v=2所对应的坐标曲线;计算
时,u,v可以用采作为曲线坐标;解出x,y作为u,v的函数;曲出xy平面上u=1,v=2所对应的坐标曲线;计算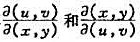 并验证它们互为倒数.
并验证它们互为倒数.
设f(x),g(x)EPIx],degf(x)>0.degg(x)>0.添上什么条件后,满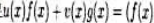
,g(x)的u(x),V(x)是唯一的.
(1) H(SX) () H(X);
(2)h(U) () h(U):
(3) H(X|Y) () H(X|YZ);
(4) H(XY) () H(X)+ H(Y):
(5) I(f(U):g(V)) () I(U;V)。
建立一个模型说明要用三级火箭发射人造卫星的道理。
(1)设卫星绕地球做匀速圆周运动,证明其速度为 R为地球半径,r为卫星与地心距离,g为地球表面重力加速度,要把卫星送上离地面600km的轨道,火箭末速v应为多少?
R为地球半径,r为卫星与地心距离,g为地球表面重力加速度,要把卫星送上离地面600km的轨道,火箭末速v应为多少?
(2)设火箭飞行中速度为v(t),质量为m(t),初速为0,初始质量m0,火箭喷出的气体相对于火箭的速度为u,忽略重力和阻力对火箭的影响。用动量守恒原理证明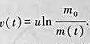 由此你认为要提高火箭的末速应采取什么措施。
由此你认为要提高火箭的末速应采取什么措施。
(3)火箭质量包括3部分:有效载荷(卫星)mp,燃料mf;结构(外壳、燃料仓等)ms,其中ms在mf+ms中的比例记作λ,一般λ不小于10%。证明若mp=0(即火箭不带卫星),则燃料用完时火箭达到的最大速度为vm=-ulnλ。已知目前的u=3km/s,取λ=10%,求vm,这个结果说明什么?
(4)假设火箭燃料燃烧的同时,不断丢弃无用的结构部分,即结构质量与燃料质量以λ和1-λ的比例同时减少,用动量守恒原理证明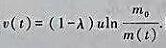 问燃料用完时火箭末速为多少,与前面的结果有何不同?
问燃料用完时火箭末速为多少,与前面的结果有何不同?
(5)(4)是个理想化的模型,实际上只能用建造多级火箭的办法一段段地丢弃无用的结构部分。记mi为第i级火箭质量(燃料和结构),λmi为结构质量(λ对各级是一样的)。有效载荷仍用mp表示。当第1级的燃料用完时丢弃第1级的结构,同时第2级点火。再设燃烧级的初始质量与其负载质量之比保持不变,比例系数为k。证明3级火箭的末速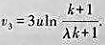 计算要使v3=10.5km/s,发射1t重的卫星需要多重的火箭(u,λ用以前的数据)?若用2级或4级火箭,结果如何?由此得出使用3级火箭发射卫星的道理。
计算要使v3=10.5km/s,发射1t重的卫星需要多重的火箭(u,λ用以前的数据)?若用2级或4级火箭,结果如何?由此得出使用3级火箭发射卫星的道理。
问题描述:给定一个赋权无向图G=(V,E),每个顶点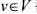 都有权值w(v).如果
都有权值w(v).如果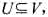 ,且对任意(u,V)∈E有u∈U或v∈U,就称U为图G的一个顶点覆盖.G的最小权顶点覆盖是指G中所含顶点权之和最小的顶点覆盖.
,且对任意(u,V)∈E有u∈U或v∈U,就称U为图G的一个顶点覆盖.G的最小权顶点覆盖是指G中所含顶点权之和最小的顶点覆盖.
算法设计:对于给定的无向图G,设计一个优先队列式分支限界法,计算G的最小权顶点覆盖.
数据输入:由文件input.txt给出输入数据.第1行有2个正整数n和m,表示给定的图G有n个顶点和m条边,顶点编号为1,2,...,n.第2行有n个正整数表示n个顶点的权.接下来的m行中,每行有2个正整数u和v,表示图G的一条边(u,v).
结果输出:将计算的最小权顶点覆盖的顶点权值和以及最优解输出到文件output.txt.文件的第1行是最小权顶点覆盖顶点权之和;第2行是最优解xi(1≤i≤n),xi=0表示顶点i不在最小权顶点覆盖中,xi=1表示顶点i在最小权顶点覆盖中.



 如果结果不匹配,请
如果结果不匹配,请 
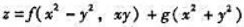 其中f(u,v)具有二阶连续偏导数,g(u)具有二阶导数,则
其中f(u,v)具有二阶连续偏导数,g(u)具有二阶导数,则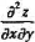 =().
=().